Understanding Option Greeks A Trader's Guide

If you've ever felt like you're just guessing with options, it's probably because you haven't met the Greeks yet. Think of them as the vital signs for your trades. These five metrics—Delta, Gamma, Theta, Vega, and Rho—tell you exactly how your options will react when things like the stock price, time, and market volatility start shifting.

Learning them is the difference between gambling and trading with a plan.

Why Understanding Option Greeks Is Crucial

Imagine trying to fly a plane without an instrument panel. No altitude, no speed, no fuel gauge... just you, the sky, and a whole lot of hope. Trading options without knowing the Greeks is a lot like that—you’re flying completely blind.

These aren't just abstract numbers for Wall Street quants. They are your real-time dashboard, giving you a clear picture of your position's risk and potential reward. Each Greek isolates one specific force that pushes an option's price up or down.

When you know what each one does, you can start building trades that actually match what you think the market will do. Expecting a big move? A period of calm? A spike in fear? There’s a way to position yourself for each scenario, and the Greeks are your guide.

Building a Foundation for Smarter Trading

Once you get a handle on the Greeks, you can move way beyond just buying simple calls and puts. This knowledge opens the door to more sophisticated, risk-defined approaches. As you get comfortable, exploring some common options trading strategies will give you a great sandbox to apply what you've learned.

Here’s why this is so important:

Precise Risk Management: You can finally put a number on your exposure to price swings, the slow burn of time decay, and shifts in volatility. This lets you hedge or adjust your position before a small problem becomes a big one.
Informed Strategy Selection: The Greeks help you pick the right tool for the job. Want to profit from a stock going nowhere? You'll want a strategy that benefits from time decay (Theta).
Enhanced Profitability: You can spot opportunities others miss by analyzing factors like implied volatility (Vega), helping you find options that might be overpriced or underpriced.

Before we dive into each one, let's get a quick lay of the land.

The Trader's Dashboard: A Quick Look at the Option Greeks

This table provides a quick, high-level overview of what each of the five primary option greeks measures, helping you grasp their individual roles before we dive deeper.

Greek	What It Measures	Key Market Factor
Delta	Sensitivity to the underlying stock's price	Price
Gamma	The rate of change of Delta	Price
Theta	The rate of time decay	Time
Vega	Sensitivity to changes in implied volatility	Volatility
Rho	Sensitivity to changes in interest rates	Interest Rates

This gives you a starting point for understanding how each Greek helps you manage a specific type of risk. Now, let’s see them in action.

This image breaks down the relationship visually, putting the most critical Greeks front and center.

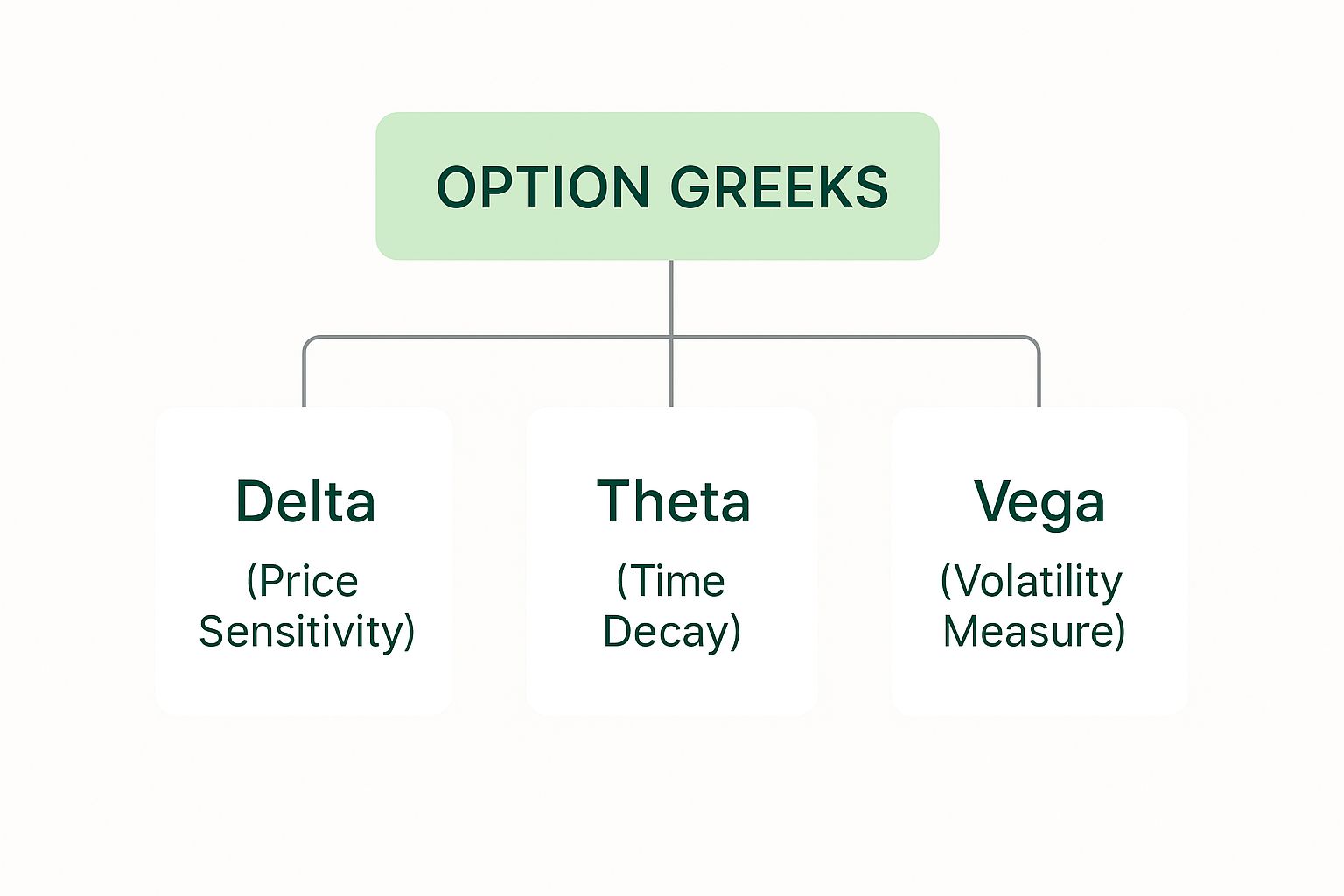
As you can see, Delta, Theta, and Vega are the big three. They represent the core risks every options trader has to watch: price, time, and volatility.

The real power of the greeks lies in their ability to work together. They provide a multi-dimensional view of risk that helps you understand not just if a position might be profitable, but how and why.

For example, you could have a trade with a great Delta (your directional bet is looking good), but if its Theta (time decay) is chewing away at your premium every single day, you could still lose money. Likewise, a sudden collapse in market volatility can crush an option's value—a risk measured by Vega.

It’s all about balancing these forces. By doing so, you can build trades with a much higher probability of success. In the sections ahead, we’ll break down each Greek, one by one.

Delta: How Options React to Price Moves

When you're getting into options, Delta is the first Greek you absolutely have to know. Think of it as the starting point for measuring an option's risk because it answers the most basic question every trader has: "How much will my option's price change if the stock moves?"

Simply put, Delta tells you an option's sensitivity to a $1 shift in the underlying stock's price. For example, if a call option has a Delta of 0.70, its price should go up by about $0.70 for every $1 the stock climbs. If the stock drops by $1, that same option will lose around $0.70 in value.

This single number is your window into directional risk. A quick glance at Delta gives you an instant feel for how exposed your position is to the market's daily swings.

Interpreting Delta for Calls and Puts

Delta isn't just one number; it lives on a spectrum, and whether it's positive or negative tells you everything about how your option relates to the stock.

Call options have a positive Delta, ranging from 0 to +1.0. This makes sense—when the stock price goes up, the value of a call option goes up with it.
Put options have a negative Delta, ranging from 0 to -1.0. This is an inverse relationship. As the stock price rises, a put option's value falls. But if the stock price drops, the put's value increases.

The size of the Delta shows you how strong that relationship is. A deep in-the-money call with a 0.95 Delta will move almost dollar-for-dollar with the stock, acting a lot like owning the shares outright. On the flip side, a far out-of-the-money put with a Delta of -0.05 will barely flinch if the stock moves a little.

Delta's Second Job: A Probability Gauge

Here’s where Delta gets really powerful. Beyond just measuring price sensitivity, Delta also serves as a rough estimate of the probability that an option will expire in-the-money (ITM).

This dual role is a game-changer for traders, especially if you're using a platform like Strike Price that's built around probability metrics.

A call option with a Delta of 0.30 doesn't just mean it will gain $0.30 if the stock rises by $1. It also implies there's roughly a 30% chance the option will be profitable at expiration.

This insight shifts trading from pure guesswork to a more strategic game of odds. Instead of just betting on a direction, you can build trades based on a calculated chance of success. This is why understanding the Greeks is so important—they quantify these sensitivities. Historically, data from sites like Optionistics.com shows that at-the-money call options on S&P 500 stocks tend to have a Delta around 0.50, suggesting a coin-flip chance of expiring ITM.

Delta in a Real-World Example

Let's ground this with a quick example. Imagine you're eyeing a call option for XYZ stock, which is currently trading at $150 a share. You're looking at a call with a $155 strike price that expires in 45 days.

The option's premium is $2.50.
The Delta for this option is 0.40.

Right away, you know two critical things:

Price Sensitivity: If XYZ stock ticks up from $150 to $151, your call option's premium will increase by about $0.40, bringing it from $2.50 to $2.90.
Probability: There's about a 40% chance that XYZ stock will be trading above your $155 strike price when the option expires.

This lets you weigh the risk and reward much more clearly. A low-Delta trade might offer a huge potential payout, but you know the odds are stacked against you. A high-Delta option, on the other hand, has a better chance of success but will cost more upfront, which limits your overall return.

If you want to go even deeper, be sure to check out our full guide on what is delta in options trading.

Gamma: The Accelerator Behind Delta

If Delta is your option's speed, Gamma is the accelerator pedal. Simple as that.

While Delta tells you how much your option’s price might change for every $1 the stock moves, Gamma tells you how fast Delta itself is going to change. It’s the rate of change of your rate of change—or for the math folks, the second derivative.

In plain English, Gamma shows you how quickly your directional exposure ramps up or slows down. A position with high Gamma is incredibly sensitive. Its Delta can swing wildly with even small moves in the stock, making Gamma a critical Greek to watch for managing trades that move fast.

This acceleration effect makes Gamma a true double-edged sword. When a stock moves your way, high Gamma creates explosive profits as your Delta climbs. But if the stock turns against you, that same acceleration can lead to devastatingly fast losses.

How Gamma Behaves in the Wild

Gamma is always a positive number for options you buy (long calls and long puts). This means as the stock price moves toward your strike—becoming more at-the-money—the absolute value of your Delta will always increase.

Let's see how this works with a quick example:

You buy a call option with a Delta of +0.40 and a Gamma of 0.05.
The stock rallies $1.
Your option's price bumps up by about $0.40, thanks to Delta.
But here's the important part: your new Delta is now +0.45 (the original 0.40 Delta + 0.05 Gamma).

Now, if the stock rallies another $1, your option will gain closer to $0.45. Gamma just juiced up your directional exposure, making your position more profitable on the next move. And if the stock had dropped instead? Your Delta would have decreased to +0.35, softening the blow on the next dollar down.

The Two Factors That Supercharge Gamma

Gamma isn't static. Its value is driven almost entirely by two things: how close the option is to its strike price and how much time is left until it expires. Nailing this relationship is key to handling what traders call "Gamma risk."

Proximity to the Strike Price: Gamma hits its peak for options that are exactly at-the-money (ATM). This is the point of maximum uncertainty—will it expire worthless or in-the-money? That uncertainty makes its Delta incredibly sensitive to price changes. Options deep in-the-money or far out-of-the-money have very low Gamma because their Deltas are already close to 1.0 or 0 and don't have much room to move.
Time to Expiration (DTE): As expiration day gets closer, Gamma for at-the-money options goes parabolic. A weekly option expiring in two days will have massively higher Gamma than a monthly option with 30 days left on the clock.

The most volatile and dangerous options are almost always short-dated, at-the-money contracts. Their high Gamma means the P&L can flip in the blink of an eye, a phenomenon that catches unprepared traders completely off guard.

Navigating the Dangers of Gamma Risk

High Gamma can be a thrill ride, but it demands your full attention. Picture holding an ATM call option on expiration day. If the stock crosses your strike price, the option’s Delta can rocket from near 0.50 to almost 1.0 (or collapse in the other direction) in just a few minutes.

That’s the essence of Gamma risk. A small, unexpected move against you can magnify your losses at an alarming rate. It's especially dangerous for anyone who sells options (short Gamma positions), as their risk accelerates exponentially against them.

Smart traders have a few ways to manage this:

Avoiding Short-Dated ATM Positions: Unless a strategy specifically calls for it, many traders will close or roll their positions before the final week to dodge that peak Gamma exposure.
Building Spreads: Strategies like vertical spreads can put a ceiling on the potential damage from Gamma. By combining a long option with a short one, you neutralize some of that explosive risk.
Monitoring and Adjusting: Active traders keep a close eye on their portfolio's net Gamma. If it gets out of line, they might hedge with shares of the stock to keep their directional risk within a comfortable range.

Ultimately, Delta tells you where you're at, but Gamma tells you how fast things are about to change. Mastering this relationship is a huge step up from making basic trades to truly managing your risk like a pro.

Theta: The Unseen Cost of Time Decay

Time is the one resource no trader can get back, and in the world of options, it has a measurable cost. This is where Theta comes in—the silent, relentless force that works against every option buyer.

Think of it as a melting ice cube. Every single day, your option’s value diminishes just because time is passing.

Theta quantifies the rate at which an option loses its extrinsic value as it approaches its expiration date. If an option has a Theta of -0.05, it means the contract is expected to lose $0.05 in value each day, assuming everything else (like the stock price and volatility) stays the same.

For option buyers, Theta is a constant headwind. You're not just betting on the stock moving your way; you're betting it will move enough to outpace this daily decay. For option sellers, however, Theta is their best friend and a primary source of profit. They collect the premium upfront and benefit as the option's value bleeds away over time.

The Acceleration of Time Decay

Here’s a critical point many new traders miss: time decay isn't linear. An option’s value doesn’t drain away at a steady, predictable rate from the day you buy it. Instead, the decay speeds up exponentially as the expiration date gets closer.

This acceleration becomes especially aggressive in the final 30-45 days of an option's life. An option with 90 days left might lose just a tiny fraction of its value each day. But an at-the-money option with only one week to go could lose a huge chunk of its value overnight.

This is precisely why buying short-term, weekly options is so risky. The Theta "burn" is at its peak, meaning you have to be right on your directional bet very quickly, or time decay will wipe out your premium.

This dynamic is the foundation of many income-generating strategies. By selling options with less than 45 days until expiration, traders can position themselves to capture the most rapid period of time decay. We cover this in more detail in our guide on using time decay in options to your advantage.

How Option Buyers and Sellers View the Greeks

The greeks are beautiful because they perfectly illustrate the opposing forces in every trade. Theta shows the zero-sum nature of options trading better than any other greek—one person's risk is another's reward. The table below breaks down these conflicting perspectives.

Greek	Perspective for Option Buyer (Long Position)	Perspective for Option Seller (Short Position)
Delta	Wants high Delta; needs the stock to move.	Wants low Delta; prefers the stock to stay still.
Gamma	Positive Gamma is good; it accelerates gains.	Negative Gamma is a risk; it accelerates losses.
Theta	Negative Theta is the enemy; time is money spent.	Positive Theta is the goal; time is money earned.
Vega	Wants high Vega; benefits from rising volatility.	Wants low Vega; benefits from falling volatility.

As you can see, the buyer and seller are on opposite sides of every single Greek. For Theta, the buyer is "short Theta," meaning its effect is negative. The seller is "long Theta," meaning its effect is positive and profitable.

A Practical Example of Theta in Action

Let's imagine you're looking at two call options on XYZ stock, which is currently trading at $100. Both options have a $100 strike price, making them at-the-money.

Option A: Expires in 90 days. Premium is $5.00. Theta is -0.02.
Option B: Expires in 15 days. Premium is $1.50. Theta is -0.08.

Option A costs more upfront, but you're only "paying" two cents per day in time decay to hold it. Option B is much cheaper, but it's bleeding value four times as fast.

As a buyer, you’d need to be extremely confident in a quick, sharp move to justify holding Option B. As a seller, Option B is the more attractive choice for an income strategy because its premium will decay much more rapidly, letting you pocket the cash sooner.

Vega: How Volatility Shapes Option Prices

While Delta and Gamma are all about price movement, Vega brings a totally different force into the game: fear and uncertainty. Technically speaking, Vega measures how sensitive an option's price is to changes in its implied volatility (IV).

Vega tells you exactly how much an option's premium will change for every 1% shift in implied volatility. Let’s say an option has a Vega of 0.10. If IV climbs from 25% to 26%, that option's price will tick up by $0.10. If IV drops by that same 1%, the premium falls by $0.10. Simple as that.

This Greek is a big deal because volatility is one of the most powerful drivers of an option's price. More uncertainty means a wider range of potential outcomes, making options more valuable to both buyers and sellers. Vega is how we measure that dynamic.

The Role of Time in Vega

Time plays a huge role in Vega, but it works the opposite way it does for Gamma. Options with more time left until expiration are much more sensitive to volatility changes.

Think of it this way: a sudden change in today's weather forecast doesn't really affect the long-term climate outlook. In the same way, a short-term spike in volatility has a much bigger impact on an option expiring this Friday than on one expiring a year from now.

This gives us a clear split:

Long-term Options (LEAPs): These contracts have high Vega. Their value is heavily tied to broad market sentiment and long-term expectations for volatility.
Short-term Options (Weeklies): These have low Vega. Their prices are mostly driven by the stock's immediate price moves (Delta and Gamma) and rapid time decay (Theta).

For any call or put option you buy, Vega is always a positive number. This means rising implied volatility is your friend—it inflates the option's premium. Falling volatility hurts you. For option sellers, the opposite is true; they want volatility to drop.

The Dreaded "Volatility Crush"

Vega becomes absolutely critical around big, scheduled events—think company earnings reports or major FDA announcements. In the days leading up to the news, uncertainty is off the charts. Nobody knows what’s going to happen, so traders bid up option prices, sending implied volatility and Vega through the roof.

Then, the moment the news drops, all that uncertainty vanishes. It doesn't even matter if the news was good or bad; the "what if" is gone.

This sudden evaporation of uncertainty causes implied volatility to plummet. We call this the "volatility crush." Countless traders have been burned by this, watching their option’s value get destroyed even when the stock moved in their favor. The gains from Delta were completely erased by the massive losses from Vega. You can get a deeper look at the mechanics in our guide on how to calculate implied volatility.

Vega in the Real World

Look at any period of major market stress, and you'll see Vega's power in action. During the COVID-19 panic in March 2020, for instance, implied volatility for the S&P 500 shot above 80%—a huge leap from its historical average of around 25%. This caused wild swings in option prices that were directly tied to their Vega.

Understanding Vega is your key to navigating these moments. It helps you protect yourself from things like a volatility crush, but it also lets you build strategies that can profit from changes in market fear. It turns one of the biggest risks in options trading into a potential opportunity.

Rho: The Hidden Force of Interest Rates

While most short-term traders don't spend much time thinking about it, Rho is the option Greek that measures how sensitive a contract is to changes in interest rates. It tells you how much an option's price should move for every 1% shift in the risk-free rate.

For anyone trading weekly or monthly options, Rho’s impact is usually tiny. A small rate change over a few weeks might only shift an option's premium by a few pennies, which is why it often gets ignored in favor of the more powerful Delta, Theta, and Vega.

But don't write it off just yet. Its importance grows dramatically with time.

Why Your Time Horizon Changes Everything

Rho packs a much bigger punch on long-term options, like Long-Term Equity AnticiPation Securities (LEAPs), which can expire more than a year out. The logic is simple: the cost of carrying an options position is more significant over longer periods, and that cost is tied directly to interest rates.

Think of it as an opportunity cost. Higher interest rates change the math on tying up capital, and this affects calls and puts differently:

Call Options: Higher rates generally make calls more valuable. Why? Because buying a call lets you control 100 shares for a fraction of the cost. The money you didn't spend on the stock can now earn a higher return at the new, beefed-up interest rate. This makes calls more attractive, so they have a positive Rho.
Put Options: On the flip side, higher rates tend to make puts less valuable. Puts are often used to hedge a short stock position. When you short a stock, you get cash, and higher rates mean you earn more interest on that cash. This makes the put hedge less necessary, so puts have a negative Rho.

Rho in a Shifting Economic Climate

In an economy where the central bank is actively changing rates, understanding Rho is no longer just an academic exercise. It gives you a complete picture of the forces moving your portfolio. The models for calculating Greeks have come a long way, and with central banks making significant rate adjustments, Rho has become a crucial part of modern risk management. To get a deeper look at this evolution, you can explore detailed insights on option greeks from Databento.

Let's say you own a LEAP call option with a Rho of 0.20. If interest rates jump by 1%, that option's price will increase by about $0.20 per share, or $20 per contract. Across a large position, that "subtle" factor can really add up.

You probably won't check Rho on every weekly trade, and that's fine. But knowing when it matters is what separates good traders from great ones. If you're a long-term investor using options or trading in a volatile rate environment, ignoring Rho means you’re missing a key piece of the puzzle.

Common Questions About Option Greeks

As traders get their feet wet with options, a few questions always seem to pop up. Nailing down these concepts is the key to building a solid foundation and actually using the greeks to your advantage.

Which Option Greek Is Most Important for a Beginner?

If you're just starting out, focus on Delta first. It’s the most intuitive of the bunch and gives you a direct feel for an option's directional risk and its rough probability of success.

Delta answers the single most important question you have at the beginning: "How much will my option's price move if the stock moves?" Once you get a handle on Delta, understanding the others like Gamma and Vega becomes much easier. Think of it as the cornerstone for assessing risk on any basic options trade.

Remember, the greeks aren't a crystal ball. They're risk-management tools that tell you how an option is currently sensitive to different market forces. They help you anticipate how your position might react if things change.

How Do Professional Traders Actually Use the Greeks?

Pros use the greeks to build and manage complex portfolios with tightly defined risks. Instead of just betting on a stock going up or down, they construct positions with very specific greek profiles that match their view of the market.

For example, a pro might set up a "delta-neutral" strategy. The goal is to create a position that isn't immediately affected by small moves in the stock price. This lets them isolate and profit from other factors, such as:

Positive Theta: Collecting daily income from time decay.
Negative Vega: Profiting from a decrease in market volatility.

They are constantly watching their portfolio's total greeks, making small adjustments with stocks or other options to keep their overall risk exactly where they want it. It's a shift from making individual bets to systematically managing a web of interconnected risks and rewards — that's the real power of understanding option greeks.

Ready to stop guessing and start trading with a statistical edge? Strike Price gives you the real-time probability metrics you need to sell covered calls and secured puts with confidence. Turn guesswork into informed action today.